Черчение

Форма многих деталей имеет плавный переход одной поверх­ности в другую (рис. 59). Для построения на чертежах контуров таких поверхностей используются сопряжения — плавный пере­ход одной линии в другую.

Для построения линии сопряжений необходимо знать центр, точки и радиус сопряжения.

Центром сопряжения является точка, равноудаленная от со­прягаемых линий (прямых или кривых). В точках сопряжений происходит переход (касание) линий. Радиусом сопряжения на­зывается радиус дуги сопряжения, с помощью которой происхо­дит сопряжение.

Рис. 59. Примеры плавного соединения поверхностей хлебницы и линий на проекции ее боковой стенки

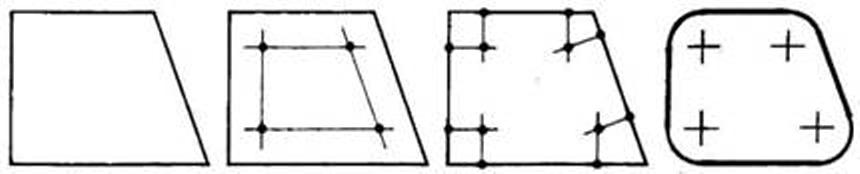
Рис. 60. Сопряжение углов на примере построения проекции боковой стенки хлебницы

Центр сопряжения должен находиться на пересечении допол­нительно построенных линий (прямых или дуг), равноудаленных от заданных линий (прямых или дуг) либо на величину радиуса сопряжения, либо на специально рассчитываемое для данного типа сопряжения расстояние.

Точки сопряжения должны находиться на пересечении задан­ной прямой с перпендикуляром, опущенным из центра сопряже­ния на заданную прямую, либо на пересечении заданной окруж­ности с прямой, соединяющей центр сопряжения с центром за­данной окружности.

Сопряжение углов. Рассмотрим последовательность сопряже­ния углов (рис. 60) на примере построения проекции боковой стенки хлебницы:

1) построим трапецию, условно принимая ее за изображение формы заготовки для стенки хлебницы;

2) найдем центры сопряжения как точки пересечения вспомо­гательных линий, равноудаленных от сторон трапеции на рас­стояние, равное радиусу сопряжения, и параллельных им;

3) найдем точки сопряжения — точки пересечений перпенди­куляров, опущенных на стороны трапеции из центров сопря­жения;

4) из центров сопряжения проведем дуги радиусом сопряже­ния от одной точки сопряжения до другой; при обводке получен­ного изображения вначале обведем дуги сопряжений, а затем — сопрягаемые линии.

Сопряжение прямой и окружности дугой заданного радиуса. Рассмотрим это на примере построения фронтальной проекции детали «Опора» (рис. 61). Будем считать, что большая часть по­строения проекции уже сделана; необходимо отобразить плавный переход цилиндрической части поверхности к плоской. Для этого необходимо выполнить сопряжение окружности (дуги окружно­сти) с прямой линией заданным радиусом:

1) найдем центры сопряжения как точки пересечения четырех вспомогательных линий: двух прямых, параллельных верхнему ребру основания «Опоры» и удаленных от нее на расстояние, равное радиусу сопряжения, и двух вспомогательных дуг, от­стоящих от заданной дуги (цилиндрической поверхности) «Опо­ры» на расстояние, равное радиусу сопряжения;

2) найдем точки сопряжения как точки пересечения: а) задан­ных прямых (ребер «Опоры») с перпендикулярами, опущенными к ним из центров сопряжения; б) заданной дуги, изображающей на чертеже цилиндрическую поверхность опоры, с прямыми, со­единяющими центры сопряжения с центром сопрягаемой дуги;

3) из центров сопряжения проводим дуги радиусом сопряже­ния от одной точки сопряжения до другой. Обводим изображе­ние.

Сопряжение дуг окружностей дугами заданного радиуса. Рассмотрим это на примере построения фронтальной проекции формы для выпечки печенья (рис. 62), имеющей плавные перехо­ды одной поверхности в другую:

1) проведем вертикальную и горизонтальные осевые линии. На них найдем центры и проведем три дуги радиусом R;

2) найдем центр сопряжения двух верхних окружностей как точку пересечения вспомогательных дуг радиусами, равными сумме радиусов заданной окружности (R) и сопряжения (R₁), т .e.R + R₁;

3) найдем точки сопряжения как точки пересечения заданных окружностей с прямыми, соединяющими центр сопряжения с центрами окружностей. Такое сопряжение называют внешним сопряжением;

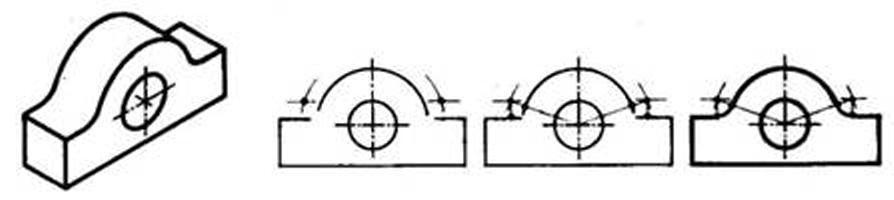
Рис. 61. Сопряжение дуги и прямых линий на примере построения фронтальной проекции детали «Опора»

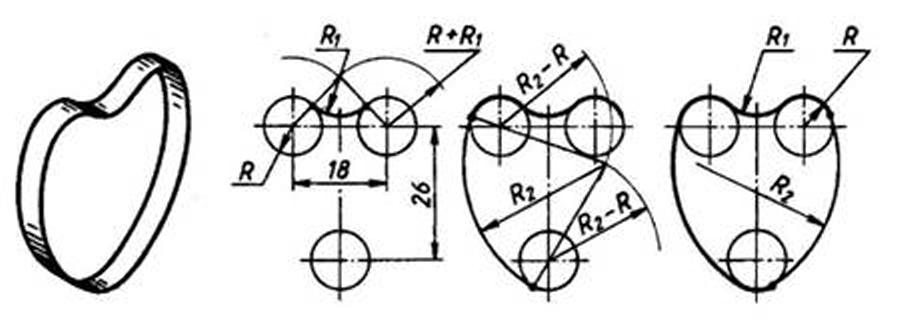
Рис. 62. Сопряжение трех дуг окружностей дугами заданных радиусов на примере
построения фронтальной проекции формы для выпечки печенья

4) построим сопряжения двух окружностей дугой заданного радиуса сопряжения R₂. Сначала найдем центр сопряжения перассечением дуг вспомогательных окружностей, радиусы которых равны разности радиуса сопряжения R₂ и радиуса окружности R, т. е. R₂ — R. Точки сопряжения получены на пересечении ок­ружности с продолжением линии, соединяющей центр сопряже­ния с центром окружности. Из центра сопряжения проведем ду­гу радиусом R₂. Такое сопряжение называется внутренним со­пряжением;

5) аналогичные построения выполним с другой стороны от оси симметрии.