Черчение

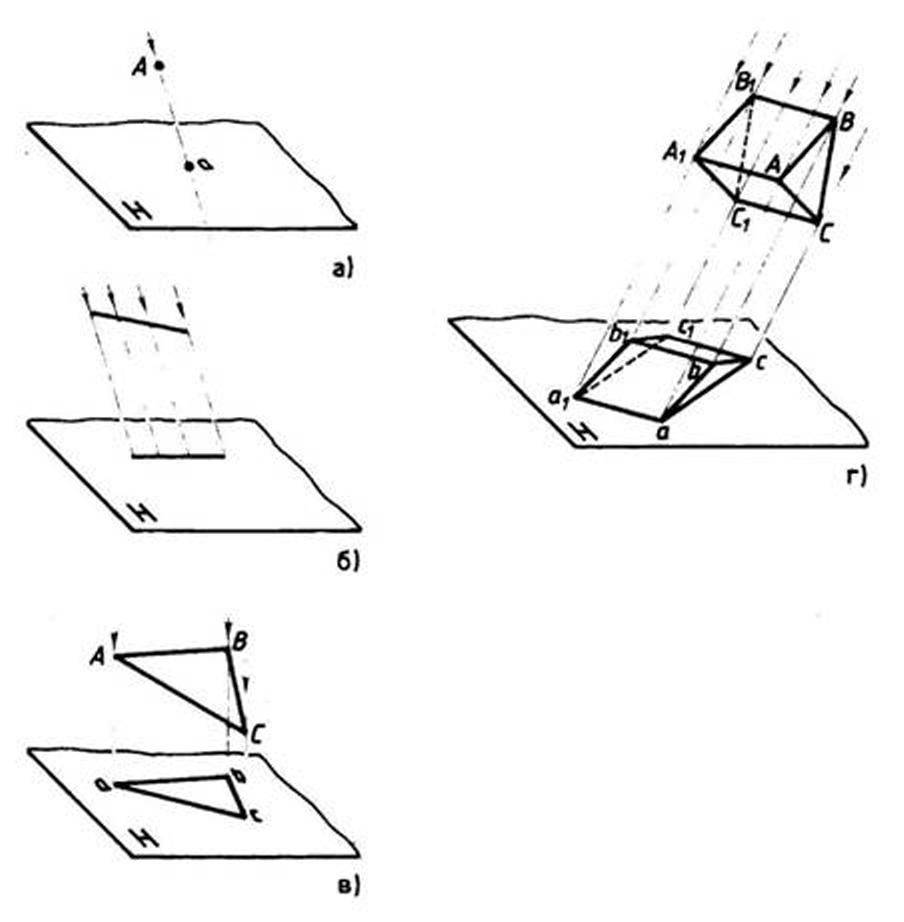
Проецирование — это процесс получения проекций предмета на какой-либо поверхности (плоской, цилиндрической, сфериче­ской, конической) с помощью проецирующих лучей.

Проецирование может осуществляться различными методами.

Методом проецирования называется способ получения изо­бражений с помощью определенной, присущей только ему сово­купности средств проецирования (центра проецирования, на­правления проецирования, проецирующих лучей, плоскостей (по­верхностей) проекций), которые определяют результат — соот­ветствующие проекционные изображения и их свойства.

Для того чтобы получить любое изображение предмета на плоскости, необходимо расположить его перед плоскостью про­екций и из центра проецирования провести воображаемые про­ецирующие лучи, пронизывающие каждую точку поверхности предмета. Пересечение этих лучей с плоскостью проекций дает множество точек, совокупность которых создает изображение предмета, называемое его проекцией. Это общее определение рассмотрим на примере проецирования точки, прямой, треуголь­ника и треугольной призмы на плоскость проекций H.

Проецирование точки (рис. 52, а). Возьмем в пространстве произвольную точку А и расположим ее над плоскостью проек­ций H. Проведем через точку А проецирующий луч так, чтобы он пересек плоскость H в некоторой точке а, которая будет являться проекцией точки А. (Здесь и в дальнейшем будем обозначать точки, взятые на предмете, прописными буквами чертежного шрифта, а их проекции — строчными.) Как видим, методом проецирования можно получить проекцию нульмерного объекта— точки.

Проецирование прямой (рис. 52, б). Представим себе прямую как совокупность точек. Используя метод проецирования, прове­дем множество параллельных проецирующих лучей через точки, из которых состоит прямая, до пересечения их с плоскостью про­екций. Полученные проекции точек составят проекцию заданной прямой — одномерного объекта.

Проецирование треугольника (рис. 52, в). Расположим тре­угольник ABC перед плоскостью H. Приняв вершины треуголь­ника за отдельные точки А, В, С, спроецируем каждую из них на плоскость проекций. Получим проекции вершин треугольника — a, b, с. Последовательно соединив проекции вершин (а и b; b и с; с и а), получим проекции сторон треугольника (ab, bc, ca). Часть плоскости, ограниченная изображением сторон треугольника abc, будет являться проекцией треугольника ABC на плоскости H Следовательно, методом проецирования можно получить проек­цию плоской фигуры — двухмерного объекта.

Проецирование призмы (рис. 52, г). Для примера возьмем наклонную треугольную призму и спроецируем ее на плоскость проекций H. В результате проецирования призмы на плоскость H получают изображения (проекции) ее оснований — треуголь­ников — abc и a₁b₁c₁ и боковых граней — прямоугольников abb₁a₁ и bcc₁b₁. Так в результате проецирования на плоскости H получают проекцию треугольной призмы. Следовательно, с помощью метода проецирования можно отобразить любой трех­мерный объект.

Рис. 52. Проецирование нуль-, одно-, двух- и трехмерных объектов: а — точка;
б — прямая; в — треугольник; г - призма

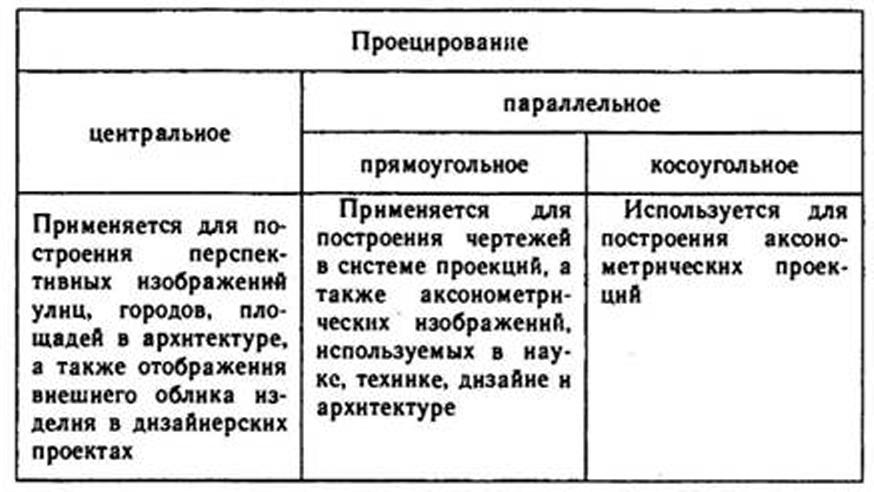
Таким образом, методом проецирования можно отобразить на плоскости любой объект (нуль-, одно-, двух- и трехмерный). В этом отношении метод проецирования является универсальным.

Сущность проецирования легче понять, если вспомнить получение изображения в кинотеатре: световой поток лампы кинопроектора проходит через пленку и отбрасывает изображение на полотно. При этом изображение на киноэкране будет в несколько раз больше изображения на кинопленке.

Существует центральное (или перспективное) и параллельное проецирование. Параллельное проецирование бывает прямо­угольным (ортогональным) или косоугольным (табл. 5).

5. Методы проецирования

Центральное проецирование (перспектива) характеризуется тем, что проецирующие лучи исходят из одной точки (S), назы­ваемой центром проецирования. Полученное изображение назы­вается центральной проекцией.

Перспектива передает внешнюю форму предмета так, как воспринимает его наше зрение.

При центральном проецировании, если предмет находит­ся между центром проецирования и плоскостью проекций, размеры проекции будут больше оригинала; если предмет расположен за плоскостью проекций, то размеры проекции станут меньше действи­тельных размеров изображаемого предмета.

Параллельное проецирование характеризуется тем, что про­ецирующие лучи параллельны между собой. В этом случае предполагается, что центр проецирования (S) удален в бесконеч­ность.

Изображения, полученные в результате параллельного про­ецирования, называются параллельными проекциями.

Если проецирующие лучи параллельны между собой и пада­ют на плоскость проекций под прямым углом, то проецирование называется прямоугольным (ортогональным), а полученные проекции — прямоугольными (ортогональными). Если проеци­рующие лучи параллельны между собой, но падают на плоскость Проекций под углом, отличным от прямого, то проецирование на­зывается косоугольным, а полученная проекция — косоугольной. При проецировании объект располагают перед плоскостью про­екций таким образом, чтобы на ней получилось изображение, несущее наибольшую информацию о форме.